Induction, Inductive Biases, and Infusing Knowledge into Learned Representations

June 22, 2020

_{^{Note: This post is a modified excerpt from the introduction to my PhD thesis.}}

Outline:

Inductive Generalization and Inductive Biases

Our goal in building machine learning systems is, with rare exceptions, to create algorithms whose utility extends beyond the dataset in which they are trained. In other words, we desire intelligent systems that are capable of generalizing to future data. The process of leveraging observations to draw inferences about the unobserved is the principle of inductionTerminological note: In a non-technical setting, the term inductive – denoting the inference of general laws from particular instances – is typically contrasted with the adjective deductive, which denotes the inference of particular instances from general laws. This broad definition of induction may be used in machine learning to describe, for example, the model fitting process as the inductive step and the deployment on new data as the deductive step. By the same token, some AI methods such as automated theorem provers are described as deductive. In the setting of current ML research, however, it is much more common for the term ‘inductive’ to refer specifically to methods that are structurally capable of operating on new data points without retraining. In contrast, transductive methods require a fixed or pre-specified dataset, and are used to make internal predictions about missing features or labels. While many ML methods are assumed to be inductive in both senses of the term, this section concerns itself primarily with the broader notion of induction as it relates to learning from observed data. In contrast, Chapters 1 and 2 involve the second use of this term, as I propose new methods that are inductive but whose predecessors were transductive 1..

Philosophical Foundations for the Problem of Induction

Even ancient philosophers appreciated the tenuity of inductive generalization. As early as the second century, the Greek philosopher Sextus Empiricus argued that the very notion of induction was invalid, a conclusion independently argued by the Charvaka school of philosophy in ancient India 2,3. The so-called “problem of induction,” as it is best known today, was formulated by 18th-century philosopher David Hume in his twin works A Treatise of Human Nature and An Enquiry Concerning Human Understanding 4,5. In these works, Hume argues that all inductive inference hinges upon the premise that the future will follow the past. This premise has since become known as his “Principle of Uniformity of Nature” (or simply, the “Uniformity Principle”), the “Resemblance Principle,” or his “Principle of Extrapolation” 6.

In the Treatise and the Inquiry, Hume examines various arguments – intuitive, demonstrative, sensible, probabilistic – that could be proposed to establish the principle of extrapolation and, having rejected them all, concludes that inductive inference itself is “not determin’d by reason.” Hume thus places induction outside the scope of reason itself, casting it therefore as non-rational if not irrational. In his 1955 work Fact, Fiction, and Forecast, Nelson Goodman extended and reframed Hume’s arguments, proposing “a new riddle of induction”7. For Goodman, the key challenge was not the validity of induction per se, but rather the recognition that for any set of observations, there are multiple contradictory generalizations that could be used to explain them.

At least among scientists, the best known formal response to the problem of induction comes from the philosopher of science Karl Popper. In Conjectures and Refutations, Popper argues that science may sidestep the problem of induction by relying instead upon scientific conjecture followed by criticism 8. Stated otherwise, according to Popper, the central goal of scientists should be to formulate falsifiable theories which can be provisionally treated as true when they survive repeated attempts to prove them false Popper’s framing is frequently used to justify the statistical hypothesis testing frameworks proposed by the likes of Neyman, Pearson, and Fisher. However, the compatibility of Popperian falsification and statistical hypothesis testing is a matter of debate 9,10,11. . Popper’s arguments may be helpful as we frame our evaluation of any specific ML system that has already been trained – and thus instantiated, in a sense, as a “conjecture” that can be refuted. However, the training process of ML systems is itself an act of inductive inference and thus relies on a Uniformity Principle in a way that Popper’s conjecture-refutation framework does not address.

This thesis is not a work of philosophy. However, I consider it important to acknowledge that the entire field of machine learning – the branch of AI concerned with constructing computers that learn from experience 12 – is predicated upon a core premise that has, for centuries, been recognized as unprovable and arguably non-rational. To boot, even if the inductive framework is accepted as valid, there are an infinite number of contradictory generalizations that are equally consistent with our training data. While these observations may be philosophical in spirit and may appear impractical, they provide a framing for extremely practical questions:

Under which circumstances can we reasonably expect the future to resemble the past, as far as our models are concerned? Given an infinite number of valid generalizations from our data – most of which are presumably useless or even dangerous – what guiding principles do we leverage to choose between them? What are the falsifiable empirical claims that we should be making about our models, and how should we test them? If we are to assume that prospective failure of our systems is the most likely outcome, as Popper would, what reasonable standards can be set to nevertheless trust ML in safety-critical settings such as healthcare?

Each of these questions will be repeatedly considered throughout the course of this thesis.

Inductive Biases in Machine Learning

As outlined above, the paradigm of machine learning presupposes the identification – a la Hume – of some set of tasks and environments for which we expect the future to resemble the past. At this point, we are thus forced to determine guiding principles – a la Goodman – that give our models strong a priori preferences for generalizations that we expect to extrapolate well into the future. When such guiding principles are instantiated as design decisions in our models, they are known as inductive biases.

In his 1980 report The Need for Biases in Learning Generalizations, Tom M. Mitchell argues that inductive biases constitute the heart of generalization and indeed a key basis for learning itself:

A key challenge of machine learning, therefore, is to design systems whose inductive biases align with the structure of the problem at hand. The effect of such efforts is not merely to endow the model with the capacity to learn key patterns, but also – somewhat paradoxically – to deliberately hamper the capacity of the model to learn other (presumably less useful) patterns, or at least to drive the model away from learning them. In other words, inductive biases stipulate the properties that we believe our model should have in order to generalize to future data; they thus encode our key assumptions about the problem itself.

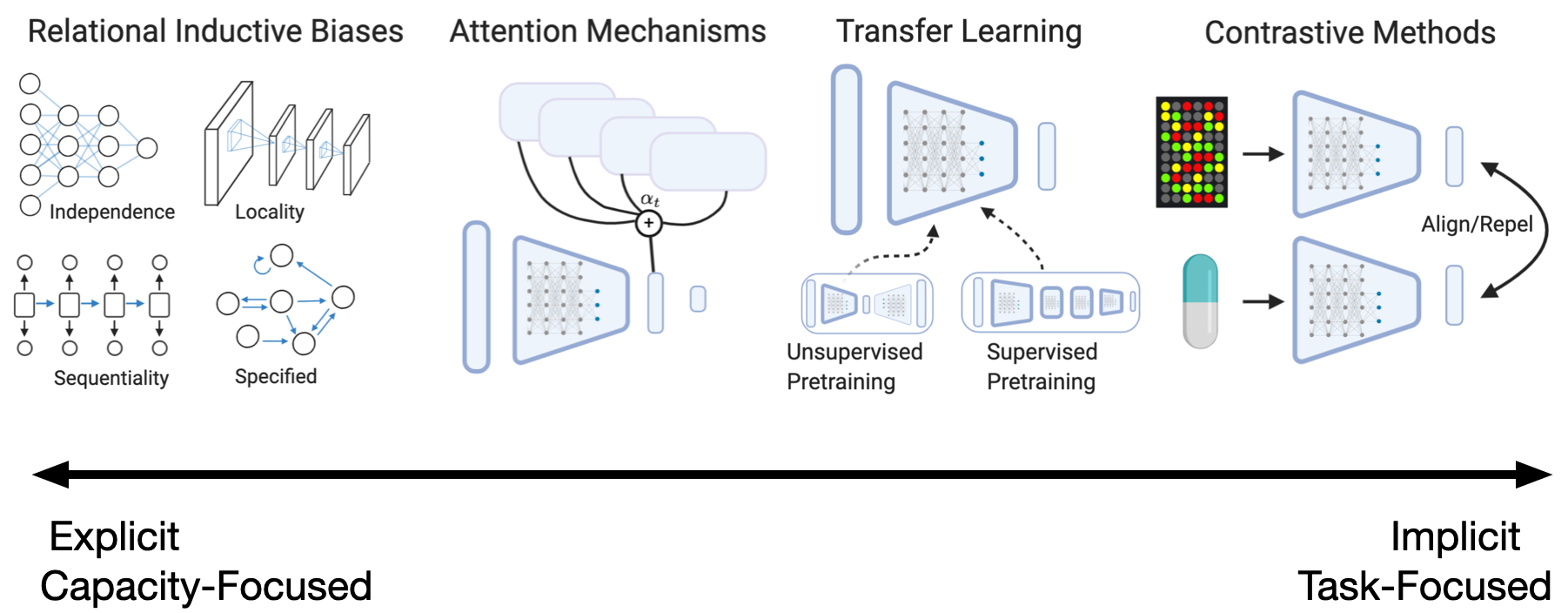
The machine learning toolkit has a wide array of methods to induce inductive biases in learning systems 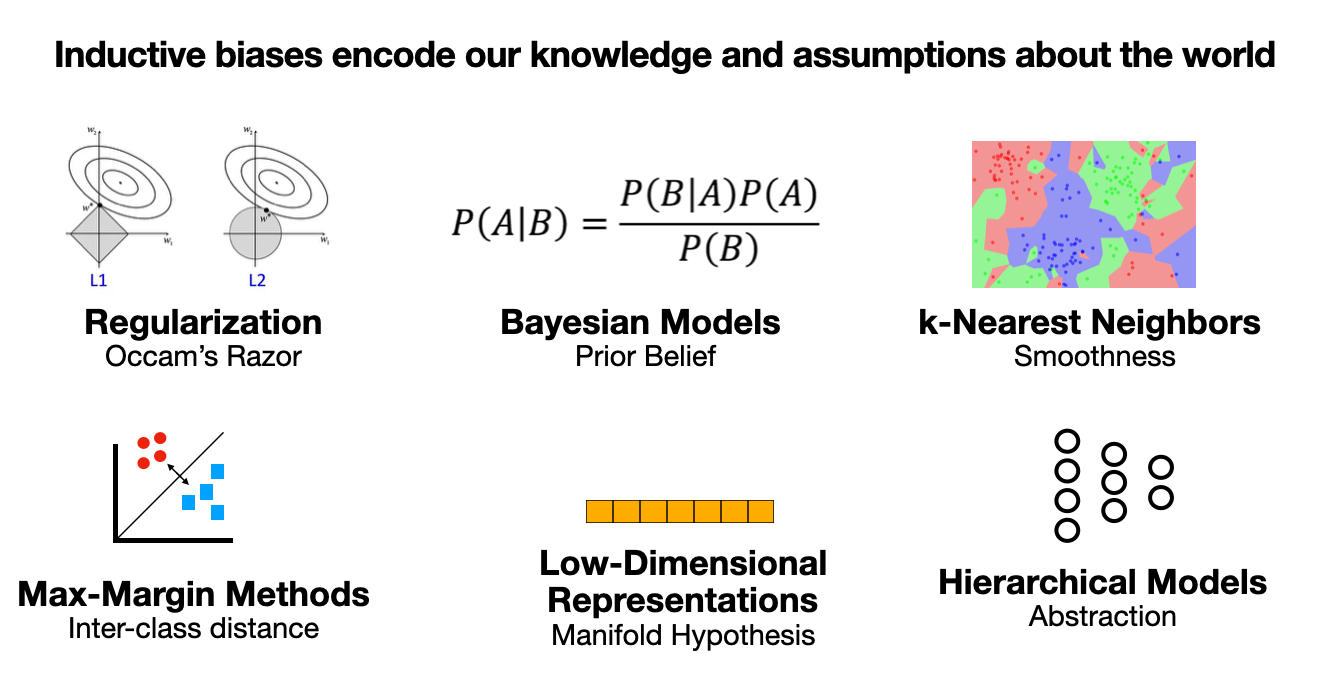⊕ . For example, regularization methods such as L1-/L2-penalties 13, dropout 14, or early stopping 15 are a simple yet powerful means to impose Occam’s razor onto the training process. By the same token, the maximum margin loss of support vector machines 16, or model selection based on cross-validation can be described as inductive biases 17,18. Bayesian methods of almost any form induce inductive biases by placing explicit prior probabilities over model parameters. Machine learning systems that build on symbolic logic, such as inductive logic programming 19, encode established knowledge into very strict inductive biases, by forcing algorithms to reason about training examples explicitly in terms of hypotheses derived from pre-specified databases of facts. As nicely synthesized in Battaglia et al, the standard layer types of modern neural networks each have distinct invariances that induce corresponding relational inductive biases; for example, convolutional layers have spatial translational invariance and induce a relational inductive bias of locality, whereas recurrent layers have a temporal invariance that induces the inductive bias of sequentiality 20. Such relational inductive biases are extremely powerful when well-matched to the data on which they are applied.

In the next section, I will introduce the neural representation learning framework – the dominant paradigm of machine learning today – and discuss inductive biases in this setting, with a special emphasis on recent tools for infusing external knowledge into the inductive biases of our models.

Learned Representations of Data and Knowledge

The performance of most information processing systems, including machine learning systems, typically depends heavily upon the data representations (or features) they employ. Historically, this meant the devotion of significant labor and expertise to feature engineering, the design of data transformations and preprocessing techniques to extract and organize discriminative features from data prior to the application of ML. Representation learning21,22 is an alternative to feature engineering, and refers to the training of learned representations of data (or knowledge graphs 23) that are optimized for utility in downstream tasks such as prediction or information retrieval.

Background on Representation Learning

Many canonical methods in statistical learning can be considered representation learning methods. For example, low-dimensional data representations with desirable properties are learned by unsupervised methods such as principal components analysis 24, k-means clustering 25, independent components analysis 26, and manifold learning methods such as Isomap 27 and locally-linear embeddings 28. Within the field of machine learning, the most popular paradigm for representation learning are neural networks21,22, which provide an extremely flexible framework that can in theory be used to approximate any continuous function 29. Over the past two decades, representation learning with neural networks has steadily outperformed traditional feature engineering methods on a large family of tasks, including speech recognition 30, image processing 31, and natural language processing 32.

A common feature of all the representation learning methods just mentioned is that they are designed to learn data representations that have lower dimensionality than the original data. This basic inductive bias is motivated by the so-called manifold hypothesis, which states that most real world data – images, text, genomes, etc. – are captured and stored in high dimensions but actually consist of some lower-dimensional data manifold embedded in that high-dimensional space.

Another desirable property of learned representations is that they be distributed representations21,22, composed of multiple elements that can be set separately from each other. Distributed representations are highly expressive: \(n\) learned features with \(k\) values can represent \(k^n\) different concepts, with each feature element representing a degree of meaning along its own axis. This results in a rich similarity space that improves the generalizability of resultant models. The benefits of distributed representations apply to any data type, but are particularly obvious from a conceptual level when considering settings such as natural language processing 33, where the initial data representation are encoded as symbols that lack any relationship with their underlying meaning. For example, the two sentences (or their equivalent triples, in a knowledge graph setting) ‘ibuprofen impairs renal function’ and ‘Advil damages the kidneys’ have zero tokens or ngrams in common. Thus, machine learning programs based only on symbols would be unable to extrapolate from one sentence to the other without relying upon explicit mappings such as ‘ibuprofen has_name Advil’, ‘impairs has_synonym damages’, etc. In contrast, the distributed representations of these sentences should, in principle, be nearly identical, facilitating direct extrapolation.

Over the past decade, neural networks have established themselves as the de facto approach to representation learning for essentially every ML problem in which their training has been shown feasible 21,22. While some neural architectures – e.g. Word2vec34 – are designed exclusively to produce embeddings that will be utilized in downstream tasks, the primary appeal of neural networks is that every deep learning architecture serves as a representation learning system. More specifically, the activations of each layer of neurons serves as a distributed representation of the input that is progressively refined in a hierarchical manner to produce representations of increased abstraction with increasing depth While even single-layer neural networks can provably approximate any continuous function, this guarantee is impractical because the proof assumes an infinite number of hidden nodes29. Deep neural networks, in contrast, allow for feature re-use that is exponential in the number of layers, which makes deep networks more expressive and more statistically efficient to train. 35,21 . In this light, a typical supervised neural network architecture of depth \(k\), for example, can arguably be best understood as a representation learning architecture of depth \(k-1\) followed by a simple linear or logistic regression.

Representations learned by neural networks have a number of desirable properties. First, neural representations are low-dimensional, distributed, and hierarchically organized, as described above. Neural networks have the ability to learn parameterized mappings that are strongly nonlinear but can still be used to directly compute embeddings for new data points. Yoshuo Bengio and others have extensively argued that neural networks have a higher capacity for generalization versus other well-established ML methods such as kernels 36,37 and decision trees 38, specifically because they avoid an excessively strong inductive bias towards smoothness; in other words, when making a new prediction for some new data point \(x\), deep representation learning methods do not exclusively rely upon the training points that are immediately nearby \(x\) in the original feature space.

Representation learning using neural networks also benefits from being modular, and therefore flexible The flexibility of neural networks doesn’t come without a price: In addition to obvious concerns about highly parameterized models and overfitting39, for example, the ease of implementing complicated DL architectures has arguably produced a research culture focused on ever-larger – and more costly40 – models that are often poorly characterised and very difficult to reproduce. 41 and extensible to design. For example, given two neural architectures that each create a distributed representation of a unique data modality, these can be straightforwardly combined into a single, fused architecture that creates a composite multi-modal representation (e.g. combining audio embeddings and visual embeddings into composite video embeddings42). Such an approach is leveraged in Chapter 2. Another example of the power afforded by the modularity of neural architectures are Generative Adversarial Networks (GANs) 43 , which learn to generate richly structured data by pitting a data-simulating ‘generator’ model against a jointly-trained ‘discrimator’ model that is optimized to distinguish real from generated data. In Supplemental Chapter 1, I demonstrate this approach using a GAN trained to simulate hip radiographs.

Taken together, neural architectures can be designed to expressively implement a broad array of inductive biases, while still allowing the network parameters to search over millions of compatible functions.

Infusing Domain Knowledge into Neural Representations

Neural networks have largely absolved the contemporary researcher of the need to hand-engineer features, but this reality has not eliminated the role of external knowledge in designing our models and their inductive biases. In this section, I compare and contrast various approaches to explicitly and implicitly infuse domain knowledge into neural representations.

The first paradigm involves the design of layers and architectures that align the representational capacity of the network with our prior knowledge of the problem domain. For instance, if we know that the data we provide have a particular property (e.g. unordered features), we can enforce corresponding constraints in our architecture (e.g. permutation invariance, as in DeepSet 44 or self-attention45 without position encodings). This is an example of a relational inductive bias 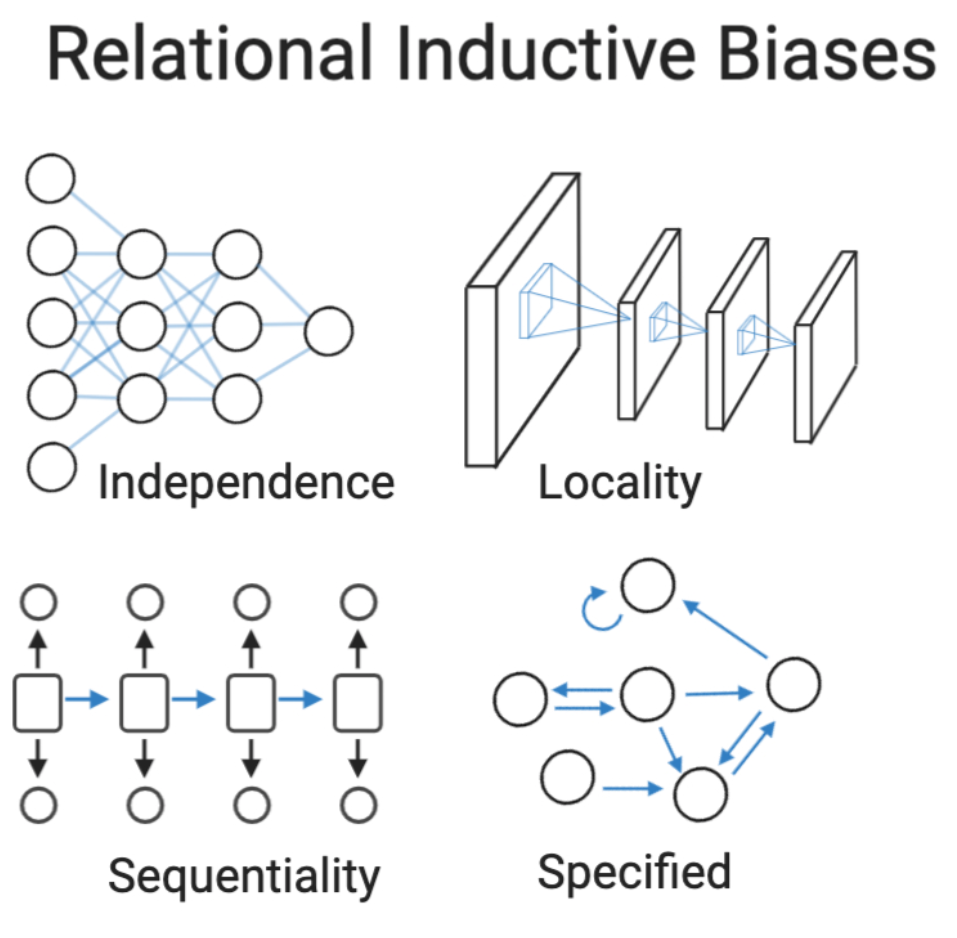⊕ 20. Relatedly, we can manually wire the network in a manner that corresponds with our prior understanding of relationships between variables. Peng et al 46 adopted this approach by building a feed forward neural network for single cell RNA-Seq data in which the input neurons for each gene were wired according to the Gene Ontology 47; this approach strictly weakens the capacity of the network, but may be useful if we have a strong prior that particular relationships would be confounding, for example. An alternative means to a similar end is to perform graph convolutions over edges that reflect domain knowledge 48.

Another explicit paradigm for infusing knowledge into neural networks is to augment the architecture with the ability to query external information. For example, models can be augmented with knowledge graphs in the form of fact triples, which they can query using an attention mechanism 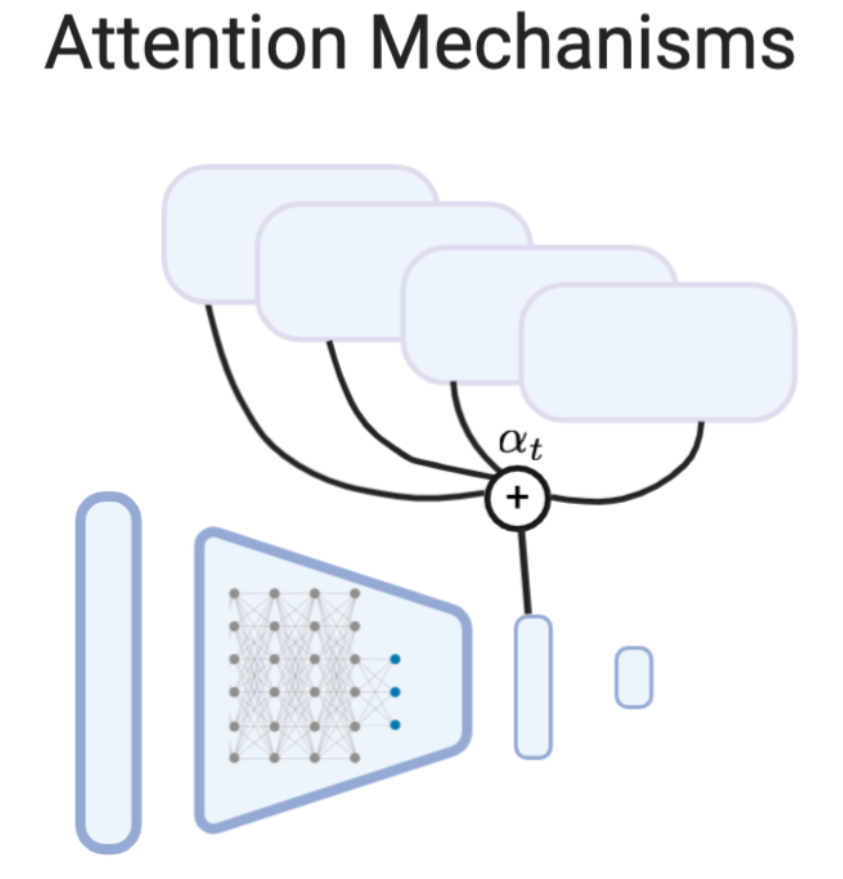⊕ 49,50. More generally, attention can be used to allow modules to incorporate relevant information from embeddings of any knowledge source or data modality. For example, 51 introduced an architecture in which a language model attends to images to generate image captions. Self-attention, or intra-attention, is an attention mechanism that allows for relating different positions within a single sequence 52,45, image 53, or other instance of input data; this allows representations to better share and synthesis information across features.

Transfer learning54,55 provides a family of methods to infuse knowledge into a learning algorithm that has been gained from a previous learning task. This is related to, but distinct from multi-task learning, which seeks to learn several tasks simultaneously under the premise that performance and efficiency can be improved by sharing knowledge between the tasks during learning. While there are many forms of transfer learning 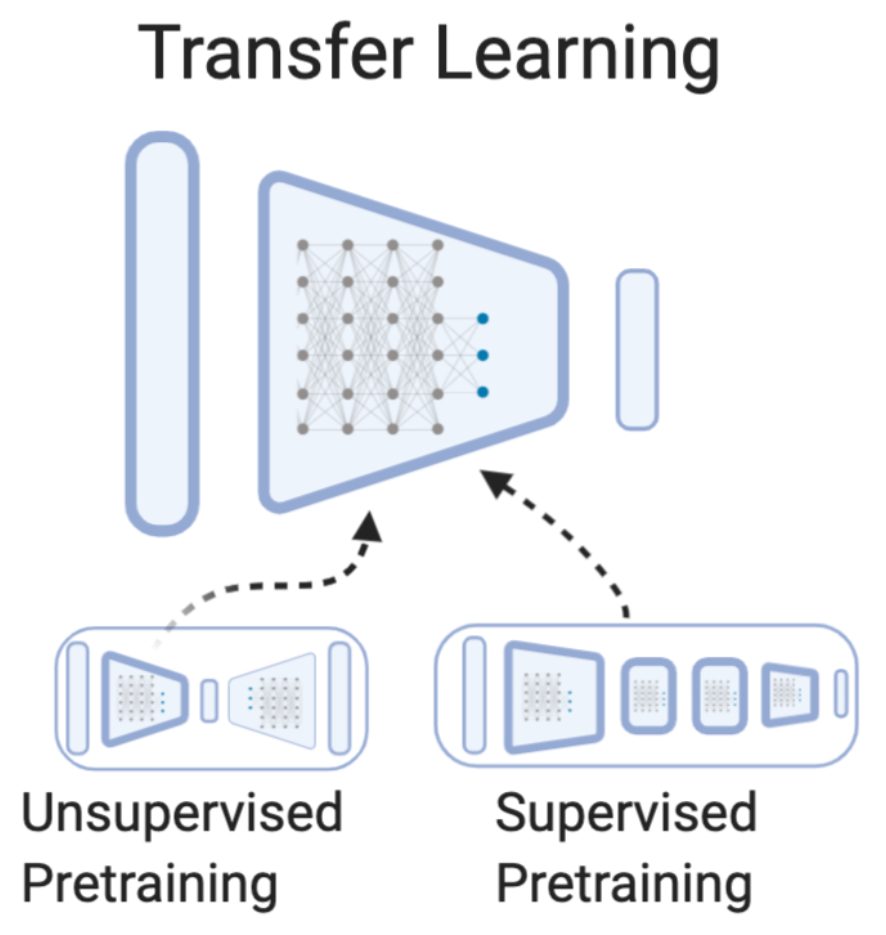⊕ 56, the canonical form in the setting of deep learning is pretraining. In pretraining, model weights from a trained neural network are used to initialize some subset of the weights in another network; these parameters can then be either frozen or “fine-tuned” with further training on a the target task. Initial transfer learning experiments were conducted using unsupervised pretraining with autoencoders Autoencoders 57 learn representations guided by the inductive bias that a good representation should be able to be used to reconstruct its raw input. They are an example of an ‘encoder-decoder’ architecture, which consist of an encoder, which take the raw input and use a series of layers to embed it into a low-dimensional space, and a decoder, which takes an embedding from the encoder and tries to construct raw data; this combined architecture is then trained in an end-to-end fashion. When the decoder is trained specifically to reconstruct the exact same input passed into the encoder, this is called an autoencoder. (Alternatively, decoders can be trained to produce related data, a prominent example being Seq2seq models that can, for example, encode a sentence from one language and decode it into another58.) Variational autoencoders 59 combine autoencoding with stochastic variational inference to build generative models that can be use for sampling entirely new data. before transferring weights to a supervised model for a downstream task; this technique is an example of inductive semi-supervised learning60. In the past decade, supervised pretraining has become very popular, with the quintessential example being the initialization of an image processing architecture with all but the final layer of a model trained on the ImageNet dataset 61. More recently, self-supervised transfer learning has received significant attention, particularly in natural language processing. In self-supervised learning, subsets of a data or feature set are masked, and neural networks are trained to predict them from remaining features. The resulting representations can then be used directly for downstream tasks, such as information retrieval, or be leveraged for transfer learning. Word embeddings 33 are arguably the first widespread instance of self-supervised transfer learning, with more recent methods including language model pretraining 62,63,45.

Contrastive learning methods 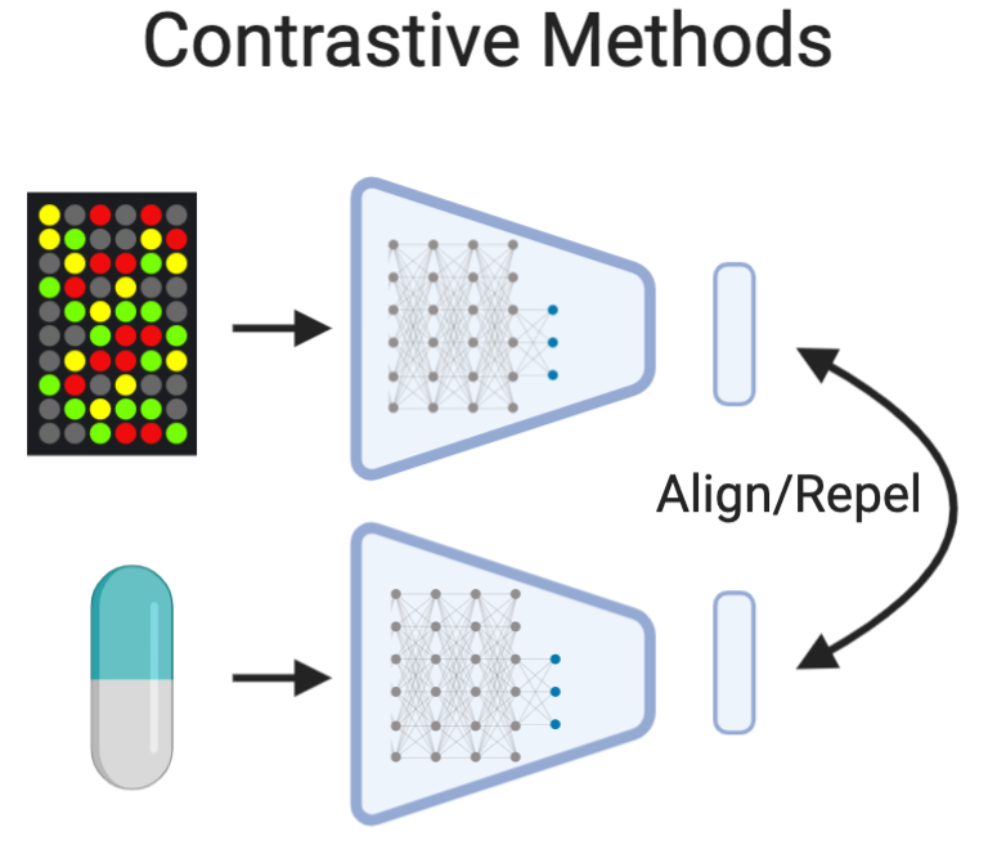⊕ learn representations by taking in small sets of examples and optimize embeddings to bring similar data together while driving dissimilar data apart. This is a form of metric learning. Early methods in this field include Siamese (missing reference) and Triplet networks 64, which were initially developed to learn deep representations of images. Recent analyses suggest that many methods developed in the past several years have failed to advance beyond triplet networks 65. Contrastive methods have been used in the pretraining step of a semi-supervised framework to achieve the current state-of-the-art in limited data image classification 66. In addition, contrastive optimization can be leveraged using multi-modal data to create aligned representations across modalities 67.

The methods described in this section can be described as a spectrum. Hand-engineered architectures are based on strong and specific prior assumptions about the problem domain, and are used to fundamentally alter the representational capacity of the network. In contrast, self-supervised and contrastive architectures make very minimal specific assumptions about the problem domain, and do nothing to alter the representational capacity of the algorithm; instead their innovation lies in devising training schemes and loss functions that will guide the network to learn underlying relationships and find a generalizable solution. In between these two extremes, augmenting networks with access to external knowledge through attention mechanisms often make the assumption that specific knowledge will be helpful, but allow the model to determine for itself which knowledge to employ. Transfer learning makes the assumption that other specific learning tasks will provide useful knowledge and experience for the target domain, but makes minimal assumptions about precisely what this knowledge would be. Despite (arguably significant) philosophical differences, these and yet other paradigms are not mutually exclusive, and share the common goal of improving generalization and data efficiency by introducing richer domain understanding into the neural networks.

Finally, while this section – and indeed several chapters of this thesis – focuses on the design of neural architectures and training curricula, the role of domain knowledge is truly inescapable when it comes to the evaluation of deployable systems. Accordingly, the topic of deployment analysis will also be a major theme of this thesis.

The current draft of my full PhD thesis can be found here.

Bibliography

1. 1.Chami, I., Abu-El-Haija, S., Perozzi, B., Ré, C., and Murphy, K. (2020). Machine Learning on Graphs: A Model and Comprehensive Taxonomy.
2. 2.Empiricus, S., and Bury, R.G. (1933). Outlines of pyrrhonism. Eng. trans, by RG Bury (Cambridge Mass.: Harvard UP, 1976), II 20, 90–1.
3. 3.Perrett, R.W. (1984). The problem of induction in Indian philosophy. Philosophy East and West 34, 161–174.
4. 4.Hume, D. (1739). A treatise of human nature (Oxford University Press).
5. 5.Hume, D. (1748). An Enquiry Concerning Human Understanding (Oxford University Press).
6. 6.Garrett, D., and Millican, P.J.R. (2011). Reason, Induction, and Causation in Hume’s Philosophy (Institute for Advanced Studies in the Humanities, The University of Edinburgh).
7. 7.Goodman, N. (1955). Fact, fiction, and forecast (Harvard University Press).
8. 8.Popper, K. (2014). Conjectures and refutations: The growth of scientific knowledge (routledge).
9. 9.Hilborn, R., and Mangel, M. (1997). The ecological detective: confronting models with data (Princeton University Press).
10. 10.Mayo, D.G. (1996). Ducks, rabbits, and normal science: Recasting the Kuhn’s-eye view of Popper’s demarcation of science. The British Journal for the Philosophy of Science 47, 271–290.
11. 11.Queen, J.P., Quinn, G.P., and Keough, M.J. (2002). Experimental design and data analysis for biologists (Cambridge University Press).
12. 12.Mitchell, T.M., and others (1997). Machine learning.
13. 13.Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological) 58, 267–288.
14. 14.Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. The journal of machine learning research 15, 1929–1958.
15. 15.Prechelt, L. (1998). Early stopping-but when? In Neural Networks: Tricks of the trade (Springer), pp. 55–69.
16. 16.Cortes, C., and Vapnik, V. (1995). Support-vector networks. Machine learning 20, 273–297.
17. 17.Girosi, F., Jones, M., and Poggio, T. (1995). Regularization theory and neural networks architectures. Neural computation 7, 219–269.
18. 18.Mitchell, T.M. (1980). The need for biases in learning generalizations (Department of Computer Science, Laboratory for Computer Science Research …).
19. 19.Muggleton, S. (1991). Inductive logic programming. New generation computing 8, 295–318.
20. 20.Battaglia, P.W., Hamrick, J.B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V., Malinowski, M., Tacchetti, A., Raposo, D., Santoro, A., Faulkner, R., et al. (2018). Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261.
21. 21.Bengio, Y., Courville, A., and Vincent, P. (2013). Representation learning: A review and new perspectives. IEEE transactions on pattern analysis and machine intelligence 35, 1798–1828.
22. 22.Goodfellow, I., Bengio, Y., and Courville, A. (2016). Representation learning. Deep Learning, 517–548.
23. 23.Bordes, A., Usunier, N., Garcia-Duran, A., Weston, J., and Yakhnenko, O. (2013). Translating embeddings for modeling multi-relational data. In Advances in neural information processing systems, pp. 2787–2795.
24. 24.Pearson, K. (1901). LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2, 559–572.
25. 25.Forgy, E.W. (1965). Cluster analysis of multivariate data: efficiency versus interpretability of classifications. biometrics 21, 768–769.
26. 26.Jutten, C., and Herault, J. (1991). Blind separation of sources, part I: An adaptive algorithm based on neuromimetic architecture. Signal processing 24, 1–10.
27. 27.Tenenbaum, J.B., De Silva, V., and Langford, J.C. (2000). A global geometric framework for nonlinear dimensionality reduction. science 290, 2319–2323.
28. 28.Roweis, S.T., and Saul, L.K. (2000). Nonlinear dimensionality reduction by locally linear embedding. science 290, 2323–2326.
29. 29.Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems 2, 303–314.
30. 30.Dahl, G., Ranzato, M.A., Mohamed, A.-rahman, and Hinton, G.E. (2010). Phone recognition with the mean-covariance restricted Boltzmann machine. In Advances in neural information processing systems, pp. 469–477.
31. 31.Hinton, G.E., Osindero, S., and Teh, Y.-W. (2006). A fast learning algorithm for deep belief nets. Neural computation 18, 1527–1554.
32. 32.Mikolov, T., Deoras, A., Kombrink, S., Burget, L., and Černockỳ, J. (2011). Empirical evaluation and combination of advanced language modeling techniques. In Twelfth Annual Conference of the International Speech Communication Association.
33. 33.Mikolov, T., Sutskever, I., Chen, K., Corrado, G.S., and Dean, J. (2013). Distributed representations of words and phrases and their compositionality. In Advances in neural information processing systems, pp. 3111–3119.
34. 34.Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
35. 35.Håstad, J., and Goldmann, M. (1991). On the power of small-depth threshold circuits. Computational Complexity 1, 113–129.
36. 36.Bengio, Y., and Monperrus, M. (2005). Non-local manifold tangent learning. In Advances in Neural Information Processing Systems, pp. 129–136.
37. 37.Bengio, Y., Delalleau, O., and Roux, N.L. (2006). The curse of highly variable functions for local kernel machines. In Advances in neural information processing systems, pp. 107–114.
38. 38.Bengio, Y., Delalleau, O., and Simard, C. (2010). Decision trees do not generalize to new variations. Computational Intelligence 26, 449–467.
39. 39.Friedman, J., Hastie, T., and Tibshirani, R. (2001). The elements of statistical learning (Springer series in statistics New York).
40. 40.Lacoste, A., Luccioni, A., Schmidt, V., and Dandres, T. (2019). Quantifying the Carbon Emissions of Machine Learning. arXiv preprint arXiv:1910.09700.
41. 41.Lipton, Z.C., and Steinhardt, J. (2018). Troubling Trends in Machine Learning Scholarship.
42. 42.Ngiam, J., Khosla, A., Kim, M., Nam, J., Lee, H., and Ng, A.Y. (2011). Multimodal deep learning.
43. 43.Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems, pp. 2672–2680.
44. 44.Zhang, Y., Hare, J., and Prugel-Bennett, A. (2019). Deep set prediction networks. In Advances in Neural Information Processing Systems, pp. 3207–3217.
45. 45.Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł., and Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems, pp. 5998–6008.
46. 46.Peng, J., Wang, X., and Shang, X. (2019). Combining gene ontology with deep neural networks to enhance the clustering of single cell RNA-Seq data. BMC bioinformatics 20, 284.
47. 47.Ashburner, M., Ball, C.A., Blake, J.A., Botstein, D., Butler, H., Cherry, J.M., Davis, A.P., Dolinski, K., Dwight, S.S., Eppig, J.T., et al. (2000). Gene ontology: tool for the unification of biology. Nature genetics 25, 25–29.
48. 48.McDermott, M., Wang, J., Zhao, W.N., Sheridan, S.D., Szolovits, P., Kohane, I., Haggarty, S.J., and Perlis, R.H. (2019). Deep Learning Benchmarks on L1000 Gene Expression Data. IEEE/ACM transactions on computational biology and bioinformatics.
49. 49.Annervaz, K.M., Chowdhury, S.B.R., and Dukkipati, A. (2018). Learning beyond datasets: Knowledge graph augmented neural networks for natural language processing. arXiv preprint arXiv:1802.05930.
50. 50.Kishimoto, Y., Murawaki, Y., and Kurohashi, S. (2018). A knowledge-augmented neural network model for implicit discourse relation classification. In Proceedings of the 27th International Conference on Computational Linguistics, pp. 584–595.
51. 51.Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., Zemel, R., and Bengio, Y. (2015). Show, attend and tell: Neural image caption generation with visual attention. In International conference on machine learning, pp. 2048–2057.
52. 52.Cheng, J., Dong, L., and Lapata, M. (2016). Long short-term memory-networks for machine reading. arXiv preprint arXiv:1601.06733.
53. 53.Parmar, N., Vaswani, A., Uszkoreit, J., Kaiser, Ł., Shazeer, N., Ku, A., and Tran, D. (2018). Image transformer. arXiv preprint arXiv:1802.05751.
54. 54.Yang, Q., and Wu, X. (2006). 10 challenging problems in data mining research. International Journal of Information Technology & Decision Making 5, 597–604.
55. 55.Pan, S.J., and Yang, Q. (2009). A survey on transfer learning. IEEE Transactions on knowledge and data engineering 22, 1345–1359.
56. 56.Zhuang, F., Qi, Z., Duan, K., Xi, D., Zhu, Y., Zhu, H., Xiong, H., and He, Q. (2019). A Comprehensive Survey on Transfer Learning. arXiv preprint arXiv:1911.02685.
57. 57.Hinton, G.E., and Salakhutdinov, R.R. (2006). Reducing the dimensionality of data with neural networks. science 313, 504–507.
58. 58.Sutskever, I., Vinyals, O., and Le, Q.V. (2014). Sequence to sequence learning with neural networks. In Advances in neural information processing systems, pp. 3104–3112.
59. 59.Kingma, D.P., and Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
60. 60.Van Engelen, J.E., and Hoos, H.H. (2020). A survey on semi-supervised learning. Machine Learning 109, 373–440.
61. 61.Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei, L. (2009). Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition (Ieee), pp. 248–255.
62. 62.Howard, J., and Ruder, S. (2018). Universal language model fine-tuning for text classification. arXiv preprint arXiv:1801.06146.
63. 63.Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
64. 64.Hoffer, E., and Ailon, N. (2015). Deep metric learning using triplet network. In International Workshop on Similarity-Based Pattern Recognition (Springer), pp. 84–92.
65. 65.Musgrave, K., Belongie, S., and Lim, S.-N. (2020). A Metric Learning Reality Check. arXiv preprint arXiv:2003.08505.
66. 66.Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. (2020). A simple framework for contrastive learning of visual representations. arXiv preprint arXiv:2002.05709.
67. 67.Deng, C., Chen, Z., Liu, X., Gao, X., and Tao, D. (2018). Triplet-based deep hashing network for cross-modal retrieval. IEEE Transactions on Image Processing 27, 3893–3903.